제곱근을 연분수로 나타낼 때 반복 주기가 홀수인 경우 세기
Problem 64
출제 일시 : 2012-02-04 18:15:54, ☕ 4
모든 제곱근은 아래와 같이 연분수로 나타낼 수 있는데, 이 때 반복되는 부분이 나타납니다.
| √N = a0 + | 1 |
||
| a1 + | 1 |
||
| a2 + | 1 |
||
| a3 + ... | |||
예를 들어서 √23을 풀어 보면,
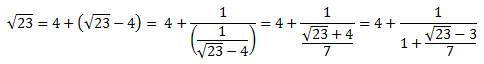
같은 식으로 계속하면 아래와 같은 모양이 됩니다.
| √23 = 4 + | 1 |
|||
| 1 + | 1 |
|||
| 3 + | 1 |
|||
| 1 + | 1 |
|||
| 8 + ... | ||||
이 과정을 상세히 보면 다음과 같습니다.
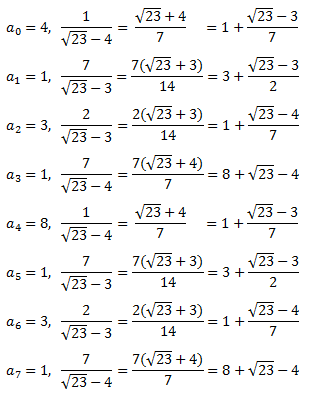
위에서 보듯이 4라는 정수부 다음에 1, 3, 1, 8 이라는 숫자가 무한히 반복되는데, 이것을 √23 = [4;(1,3,1,8)] 과 같이 표시하기로 합니다.
이런 식으로 해서 무리수인 제곱근들을 연분수로 나타내면 다음과 같이 됩니다.
| √2 | = | [1;(2)], 주기=1 |
| √3 | = | [1;(1,2)], 주기=2 |
| √5 | = | [2;(4)], 주기=1 |
| √6 | = | [2;(2,4)], 주기=2 |
| √7 | = | [2;(1,1,1,4)], 주기=4 |
| √8 | = | [2;(1,4)], 주기=2 |
| √10 | = | [3;(6)], 주기=1 |
| √11 | = | [3;(3,6)], 주기=2 |
| √12 | = | [3;(2,6)], 주기=2 |
| √13 | = | [3;(1,1,1,1,6)], 주기=5 |
반복 주기가 홀수인 경우는 N ≤ 13 일 때 모두 4번 있음을 볼 수 있습니다.
그러면 N ≤ 10000 일 때 반복 주기가 홀수인 경우는 모두 몇 번이나 있습니까?
