제곱근 2는 아래와 같은 연분수의 꼴로 나타낼 수 있습니다.

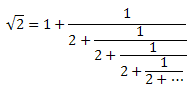
연분수에서 이렇게 끝없이 반복되는 부분은 √2 = [1;(2)] 처럼 나타낼 수 있는데, 여기서 (2)는 숫자 2가 반복됨을 뜻합니다. 같은 방법으로 √23은 [4;(1,3,1,8)] 이 됩니다.

이 연분수의 부분 합을 구하면, 해당 제곱근의 훌륭한 근사값으로 쓸 수 있습니다. √2의 수렴 과정을 보겠습니다.

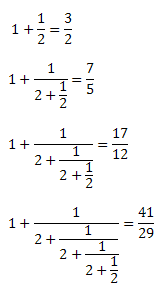
이런 식으로 처음 10번에 해당하는 값은 다음과 같이 됩니다.

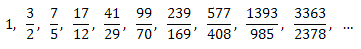
정말 놀라운 사실은, 가장 중요한 수학 상수 중 하나인 e가 다음과 같은 연분수 꼴로 나타내어진다는 것입니다.

e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...]

이 경우 수렴 과정의 처음 10번은 이렇습니다.

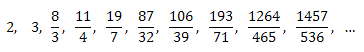
여기서 열번째 값의 분자 자릿수를 모두 더하면 1+4+5+7 = 17이 되는 것을 알 수 있습니다.

그러면 e의 100번째 연분수 확장 값의 분자 자릿수를 모두 더하면 얼마가 됩니까?