마방진 성질을 갖는 5각 도형에서 얻을 수 있는 16자리 수의 최댓값 구하기
Problem 68
출제 일시 : 2012-02-04 18:21:02, ☕ 5
아래와 같이 마방진과 유사한 성질을 가진 도형이 있습니다. 1부터 6까지의 수가 한 번씩만 사용되었고, 선을 따라 합을 구하면 항상 9가 됩니다.
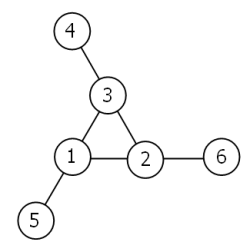
바깥으로 뻗친 가지 중에서 가장 수가 낮은 것부터 시작해서 직선들을 시계방향으로 돌아가며 나열하면, 도형의 모양을 수로 나타낼 수 있습니다. 위 그림의 예를 들면 4,3,2; 6,2,1; 5,1,3 과 같이 됩니다.
위 도형으로는 네 가지 다른 합계를 가지도록 배열할 수 있는데, 다음과 같은 여덟 개의 풀이가 존재합니다.
| 합계 | 풀이 |
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
하나의 풀이에 대해서 각 수를 모두 이어붙이면 9자리의 수를 만들 수 있고, 그 중에서 가장 큰 것은 432621513이 됩니다.
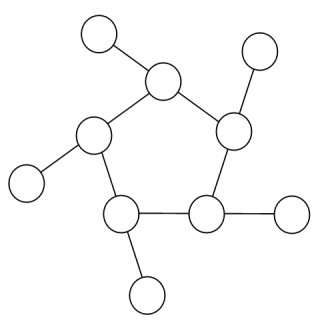
이제 아래와 같은 도형에다 마방진의 성질을 가지도록 1부터 10까지의 수를 채우고, 같은 방식으로 풀이 수를 이어붙이면 16자리 또는 17자리의 수가 만들어집니다. 이 때, 16자리 수 중에서 가장 큰 것은 무엇입니까?