정육면체를 가지고 3 × 2 × 1 크기인 직육면체의 겉면을 모두 덮으려면 최소 22개가 필요합니다.

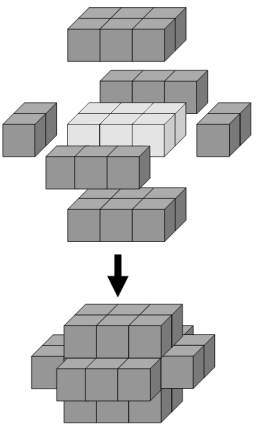
이렇게 만든 입체에 다시 한 겹을 더해서 보이는 면을 전부 덮으려면 정육면체 46개가 필요하고, 세 겹째는 78개, 네 겹째는 118개가 있어야 합니다.

하지만 5 × 1 × 1 크기의 직육면체는 처음 한 겹을 덮는 데에 22개가 필요하고, 같은 식으로 해 보면 5 × 3 × 1, 7 × 2 × 1, 11 × 1 × 1 크기의 직육면체 모두 46개가 필요합니다.

이제 겉면에 한 겹을 두르는데 필요한 정사각형의 갯수 중 n이 포함되는 직육면체의 가짓수를 C(n)이라 하겠습니다. 즉 C(22) = 2, C(46) = 4, C(78) = 5, C(118) = 8 이 됩니다.

이랬을 때 C(n) = 10을 만족하는 n의 최솟값은 154 입니다.

C(n) = 1000 인 최소의 n은 얼마입니까?

(번역 도움: cfranck님)