ABC는 내각이 모두 120도 미만인 삼각형입니다. 또, 삼각형 내부의 어떤 점 X에 대해 XA = p, XC = q, XB = r 입니다.

페르마는 토리첼리에게 p + q + r 값이 최소화 되는 점 X의 위치를 구해보라고 했습니다.

이에 토리첼리는 만일 삼각형 ABC의 각변에 정삼각형 AOB, BNC, AMC를 만들면, 세 정삼각형의 외접원은 삼각형내의 한 점 T에서 만난다는 것을 증명할 수 있었습니다. 게다가 토리첼리/페르마 포인트라고 부르는 이 점 T는 p + q + r 값을 최소화 한다는 것까지도 증명했습니다. 더 놀라운 것은, 합이 최소라면 AN = BM = CO = p + q + r 이고 선분 AN, BM, CO가 모두 점 T를 지납니다.

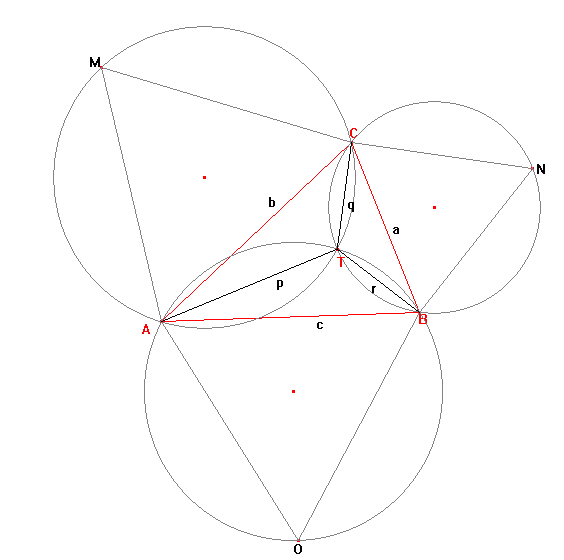
만일 합이 최소면서 a, b, c, p, q, r이 모두 자연수라면 이 삼각형 ABC를 토리첼리 삼각형이라고 합니다. 예를 들어, a = 399, b = 455, c = 511 은 토리첼리 삼각형이고 p + q + r = 784 입니다.

토리첼리 삼각형에서 생길 수 있는 서로 다른 모든 p + q + r ≤ 120000 값의 합을 구하세요.