양과 음의 정수로 이루어진 삼각 배열의 내부에서 원소의 합이 최소가 되는 삼각 배열을 찾고자 합니다.

아래 보기에서, 빨간 삼각형으로 표시된 부분 삼각 배열의 합은 -42로 이 조건을 충족합니다.

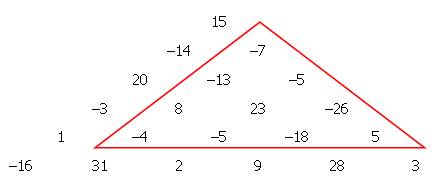
이제 1000 줄짜리 삼각 배열을 만들어 봅시다. 그러기 위해서는 500500 개의 유사 난수가 필요합니다. 선형 합동 생성기(Linear Congruential Generator)를 이용하여 ±2¹⁹ 범위의 유사 난수 s_k를 다음과 같이 생성합니다:

t := 0
for k = 1 up to k = 500500:
    t := (615949*t + 797807) modulo 2²⁰
    s_k := t−2¹⁹

따라서: s₁ = 273519, s₂ = −153582, s₃ = 450905 이렇게 생성됩니다.

그 다음 생성된 유사 난수를 이용하여 다음과 같이 삼각 배열을 만듭니다:

부분 삼각 배열은 배열의 어디에서나 시작할 수 있고 원하는 만큼 아래로 확장할 수 있습니다. 바로 아래 정수 두 개, 그 아래 정수 세 개, 이런 식입니다.
"부분 삼각 배열 합"을 부분 삼각 배열에 포함된 모든 원소의 합이라고 정의합니다.
이 삼각 배열에서 최소 "부분 삼각 배열 합"을 구하세요.