I_r은 원점을 중심으로 하는 반지름이 r인 원 x² + y² < r² 안의 정수 좌표점 (x,y)의 집합입니다.

반지름이 2일 때, I₂는 다음 9 개의 점을 (0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1), (1,-1) 포함합니다. 내부에 원점을 포함하고 세 꼭지점이 모두 I₂에 속하는 삼각형은 8 개가 있습니다. 아래에 그 중 두 개가 그려져 있습니다. 나머지는 이 둘을 회전시켜서 얻을 수 있습니다.

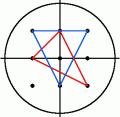
반지름이 3일 때, 내부에 원점을 포함하고 모든 꼭지점이 I₃에 속하는 삼각형은 360 개입니다. I₅라면 그 수는 10600개입니다.

내부에 원점을 포함하고 세 꼭지점이 모두 I₁₀₅에 속하는 삼각형은 몇 개입니까?