민코프스키 합
Problem 228
출제 일시 : 2020-10-19 00:02:01, ☕ 14
Sn은 보통의 n변 다각형(또는 모양)으로 꼭지점 vk (k = 1,2,…,n)의 좌표가 다음과 같습니다:
| xk = cos( 2k-1/n ×180° ) | |
| yk = sin( 2k-1/n ×180° ) |
각각의 Sn은 둘레와 안쪽 모든 점을 포함하는 채워진 모양으로 해석됩니다.
두 모양 S와 T의 민코프스키(Minkowski) 합 S+T는 T의 모든 점에 S의 모든 점을 더한 결과입니다. 점의 덧셈은 다음과 같이 좌표방식으로 수행됩니다: (u, v) + (x, y) = (u+x, v+y).
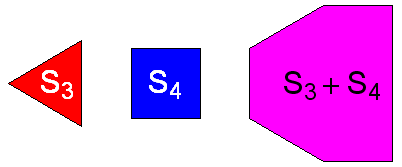
예를 들어, S3와 S4의 합은 아래에 분홍색으로 보이는 6변 모양입니다:
S1864 + S1865 + … + S1909에는 변이 몇 개입니까?
