다다미는 일본식 직사각형 돗자리로 방 바닥을 겹치지 않고 완전히 덮는데 사용됩니다.

사용 가능한 다다미가 1×2 크기 뿐이라고 가정하면, 덮을 수 있는 방의 모양과 크기는 분명히 어떤 제약이 있습니다.

이번 문제에서는, 정수 단위 치수 a, b와 짝수 크기 s = a·b를 가진 직사각형 방만 고려합니다.
여기서 '크기'는 방의 바닥 면적을 나타냅니다. 여기에 일반성을 잃지 않고, a ≤ b 조건을 추가할 수 있습니다.

다다미를 깔 때 따라야 하는 한 가지 규칙이 있습니다; 서로 다른 돗자리 네 개의 모서리가 한 점에서 만나지 않아야 합니다.
예를 들어, 아래 4×4 방을 덮는 두 가지 배치가 있습니다:

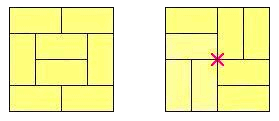
왼쪽 배치는 허용되는 반면에, 오른쪽 배치는 허용되지 않습니다: 중앙의 빨간 "X"표시는 네 돗자리가 만나는 점을 표시한 것입니다.

이 규칙 때문에, 어떤 짝수 크기 방은 다다미로 덮을 수 없습니다: 이 방을 '돗자리를 깔 수 없는 방'이라 하겠습니다.
또, T(s)를 크기가 s인 '돗자리를 깔 수 없는 방'의 수로 정의합니다.

가장 작은 '돗자리를 깔 수 없는 방'의 크기는 s = 70이고 치수는 7×10입니다.
크기 s = 70의 다른 방은 모두 돗자리를 깔 수 있습니다; 그 방은 1×70, 2×35, 5×14입니다.
따라서, T(70) = 1입니다.

비슷하게, 크기 s = 1320인 '돗자리를 깔 수 없는 방'은 다음 5개가 있어서 T(1320) = 5입니다:
20×66, 22×60, 24×55, 30×44, 33×40.
사실, 크기 s = 1320는 T(s) = 5인 가장 작은 방의 크기입니다.

T(s) = 200인 가장 작은 방의 크기 s를 구하세요.