쿼드트리(quadtree) 부호화를 이용하면 2^N×2^N크기의 흑백 영상을 비트열(0과 1로된 문자열)로 표현할 수 있습니다. 이 비트열은 왼쪽에서 오른쪽으로 다음과 같이 해석합니다:

• 첫 비트는 온전한 2^N×2^N영역을 다룹니다;
• "0"은 분할을 나타냅니다:
  현재 2ⁿ×2ⁿ영역을 크기 2^n-1×2^n-1의 하부 영역 4개로 나뉩니다,
  다음 비트들은 좌상단, 우상단, 좌하단, 우하단 하부 영역을 순서대로 기술합니다;
• "10"은 현재 영역이 모두 흑색 픽셀로만 되어 있음을 나타냅니다;
• "11"은 현재 영역이 모두 백색 픽셀로만 되어 있음을 나타냅니다.

아래의 4×4 영상을 봅시다.(색상 표시는 분할이 일어날 수 있는 곳입니다):

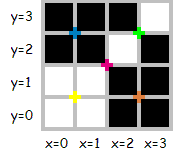
위 영상은 여러 가지 비트열로 기술될 수 있습니다, 예를 들면:
"001010101001011111011010101010", 이 비트열의 길이는 30입니다, 또는
"0100101111101110", 이 비트열의 길이는 16이고, 위 영상으로 얻을 수 있는 최소 길이입니다.

N이 자연수일 때, D_N을 다음과 같은 배색을 가진 크기 2^N×2^N의 영상으로 정의합니다:

• 좌하단 픽셀의 좌표는 x = 0, y = 0입니다,
• (x - 2^N-1)² + (y - 2^N-1)² ≤ 2^2N-2이라면 흑색 픽셀이고,
• 다른 경우에는 백색 픽셀입니다.

D₂₄ 영상을 기술하는 비트열의 최소 길이는 얼마입니까 ?