C(x,y)는 네 점 (x, y), (x, y+1), (x+1, y), (x+1, y+1)을 지나는 원입니다.

m과 n이 자연수일 때, E(m,n)는 다음 m·n개의 원으로 구성된 배치입니다:
{ C(x,y): 0 ≤ x < m, 0 ≤ y < n, 여기서 x와 y는 정수입니다 }

E(m,n)의 오일러 일주는 각 원호를 딱 한 번씩만 지나는 닫힌 경로입니다.
E(m,n)에 대한 그런 경로는 많이 있지만, 여기서는 교차하지 않는 경로에만 관심있습니다: 비교차 경로는 정수점에서 만나기는 하지만 교차하지는 않습니다.

아래 그림은 E(3,3)과 그 배치의 오일러 일주의 한 예입니다.

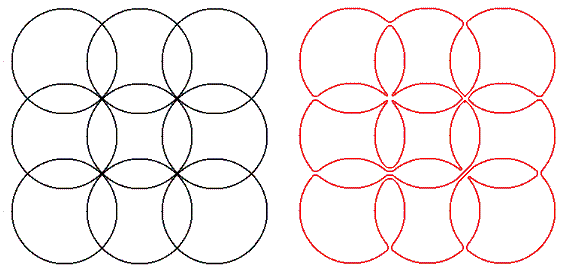
L(m,n)을 E(m,n)의 오일러 일주의 개수라고 하면.
예를 들어, L(1,2) = 2, L(2,2) = 37이고 L(3,3) = 104290입니다.

L(6,10) mod 10¹⁰ 값을 구하세요.