정수 좌표를 가진 아래 네 점을 고릅니다:
A(a, 0), B(b, 0), C(0, c), D(0, d), 여기서 0 < a < b이고 0 < c < d입니다.
또한, 선분 AC위의 정수 좌표 점 P를 잡아 세 삼각형 ABP, CDP, BDP가 모두 닮은 삼각형이 되도록 합니다.

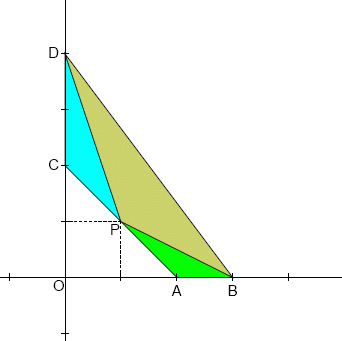
a=c일 때만 세 삼각형이 닮을 수 있다는 것은 쉽게 증명할 수 있습니다.

그래서, a=c라 하면, 세 삼각형 ABP, CDP, BDP를 모두 닮게 하는 AC위의 정수 좌표 점 P가 최소 하나 이상 존재하는 트리플 (a,b,d)를 찾습니다.

예를 들어, (a,b,d)=(2,3,4)일 때, 점 P(1,1)이 위 조건을 만족한다는 것은 쉽게 알 수 있습니다. 트리플 (2,3,4)과 (2,4,3)는 비록 점 P(1,1)가 공통이지만 서로 다른 것으로 간주되니 주의하세요.

b+d < 100일 때, 그런 점 P가 존재하는 서로 다른 트리플 (a,b,d)는 92개가 있습니다.
b+d < 100 000일 때, 그런 점 P가 존재하는 서로 다른 트리플 (a,b,d)는 320471개가 있습니다.

b+d < 100 000 000일 때, 그런 점 P가 존재하는 서로 다른 트리플 (a,b,d)는 몇 개입니까?