다음 게임은 조합 게임 이론의 전형적인 예입니다:

두 선수는 한 줄로 연결된 $n$개의 흰색 정사각형을 가지고 시작하며 차례대로 진행합니다.
선수는 자기 차례에 연속적인 흰색 정사각형 두 개를 골라서 검은색으로 칠합니다.
자기 차례에 더 할 게 없는 선수가 집니다.

• $n = 1$: 아무 것도 할 수 없기 때문에 자동으로 첫 선수가 집니다.
• $n = 2$: 단 한 수만 가능하므로, 그 수를 둔 뒤에 두 번째 선수가 집니다.
• $n = 3$: 두 수가 가능하지만, 어떤 수를 두더라도 두 번째 선수가 지는 상황이 됩니다.
• $n = 4$: 첫 선수는 세 수가 가능하고, 중앙의 두 정사각형을 칠해서 게임에서 이길 수 있습니다.
• $n = 5$: 첫 선수는 네 수가 가능하고(아래 빨간색), 어떤 수를 두더라도 두번째 선수가 이깁니다(파란색).

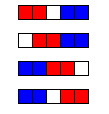
그래서, $1 \le n \le 5$일 때, 첫 선수가 무조건 이기는 $n$의 값은 3개가 있습니다.
비슷하게, $1 \le n \le 50$일 때, 첫 선수가 무조건 이기는 $n$의 값은 40개가 있습니다.

$1 \le n \le 1 000 000$일 때, 첫 선수가 무조건 이기는 $n$의 값은 몇 개가 있습니까?