달나라 시대가 열리고, 땅을 자유롭게 얻을 수 있습니다만 한가지 조건이 있습니다. 말뚝을 박아 경계를 구획한 땅에 벽을 세워야 하는데, 달에 벽을 세우는 데는 비용이 많이 듭니다. 모든 나라는 500 m x 500 m 정사각형 영역이 할당되지만 벽을 세우는 영역만 소유합니다. 직사각형 격자에 1미터 간격으로 251001개의 기둥이 박혀있습니다. 벽은 기둥에서 기둥으로 똑바로 연결한 직선으로만 만들어져야 합니다.

물론 큰 나라들은 250 000 m² 영역 전체를 둘러싸는 벽 2000 m를 건설했습니다. 작은 나라인 그랜드 펜윅 공국은 예산이 부족해서 왕립 프로그래머인 당신에게 어떤 모양의 벽이 최고의 둘러 싸인 면적/벽의 길이 비율을 얻을 수 있는지 계산해주기를 요청해왔습니다.^역주)

당신은 종이에 몇 가지 예비 계산을 했습니다. 2000 m의 벽으로 250 000 m² 영역을 둘러 싸면 둘러 싼 면적/벽의 길이 비율은 125입니다.
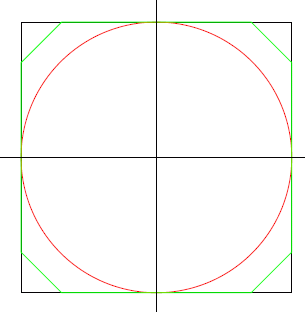
비록 허용되는 것은 아니지만, 이게 좀 더 좋아질 수 있는 구상을 얻기 위해: 만일 정사각형 영역의 안에 네 변을 접하는 내접원을 만든다면 원의 면적은 π*250² m²이고 둘레는 π*500 m이므로, 둘러 싼 면적/벽의 길이 비율은 역시 125입니다..

그러나, 정사각형에서 길이 75 m, 75 m, 75√2 m인 삼각형 네 개를 잘라내면 전체 면적은 238750 m²이고 둘레는 1400+300√2 m입니다. 따라서, 둘러 싼 면적/벽의 길이 비율은 130.87이고 전보다 현저하게 더 높은 값입니다.

둘러 싼 면적/벽의 길이 비율의 최댓값을 구하세요.
답은 소수점이하 8자리까지 반올림해서 abc.defghijk 형태로 제출하세요.

역주) 그랜드 펜윅 공국, 아일랜드계 미국인 작가 레너드 위벌리(Leonard Wibberley)의 냉전 풍자 소설 6부작에 나오는 유럽의 가상 국가. 그랜드 펜윅 공국은 길이가 8km, 너비가 5km를 넘지 않는 매우 작은 나라로 묘사되며 북 알프스 있다. 소설은 그랜드 펜윅 공국이 초강대국과 직면하여 승리하는 내용으로 단순한 풍자를 넘어서 핵 군비 경쟁, 핵무기 일반, 미국 정치를 포함한 현대 정치와 세계 상황에 대한 논평을 포함한다. '달나라의 생쥐(The Mouse on the Moon)'는 그 중 3편의 제목이다.