N×N크기의 정사각형 게임판 모든 칸에 원반이 놓여있습니다. 각 원반의 한 면은 검은 색이고 반대 면은 흰 색입니다.

매 차례에, 특정 원반을 골라서 같은 줄에 있는 모든 원반, 같은 칸에 있는 모든 원반을 뒤집습니다: 그러면 2×N-1개의 원반이 뒤집히게 됩니다. 모든 원반이 흰 색면을 보이면 게임이 끝납니다. 다음은 5×5 게임판에서의 게임 예입니다.

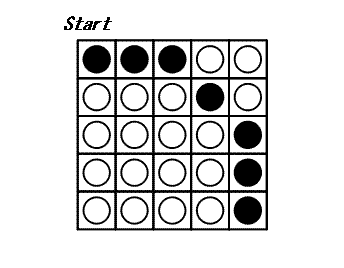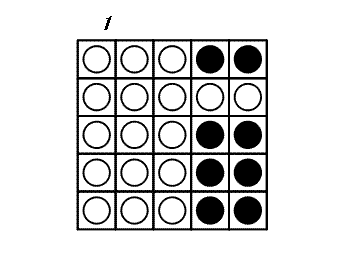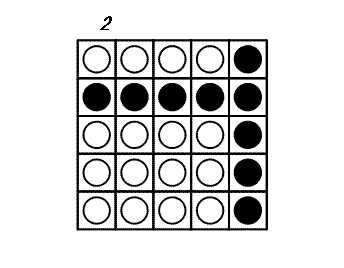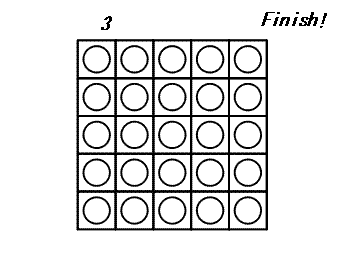
이 게임을 끝내기 위해서는 최소 3차례가 필요합니다.

N×N게임판의 가장 왼쪽 아래 원반의 좌표는 (0,0)이고;
가장 오른쪽 아래 원반의 좌표는 (N-1,0)이며 가장 왼쪽 위 원반의 좌표는 (0,N-1)입니다.

C_N은 N×N 게임판의 원반을 다음과 같이 배치한 것입니다:
$N - 1 \le \sqrt{x^2 + y^2} \lt N$를 만족하는 좌표 (x,y)에 있는 원반은 검은 색이고, 그렇지 않으면 흰 색입니다. 위에 보여진 것은 C₅입니다.

C_N에서 게임을 끝내기 위해 필요한 최소 횟수를 T(N)이라 합니다. 만일 C_N이 절대로 안 끝나는 게임이라면 T(N) = 0 입니다.
T(5)=3입니다. 또한 T(10)=29이고 T(1 000)=395253입니다.

$\sum \limits_{i = 3}^{31} {T(2^i - i)}$ 값을 구하세요.