다음은 네델란드 수학자 브루인(N.G. de Bruijn)의 은화 게임을 변형한 것입니다:

정사각형 타일로 이루어진 띠 위의 각 정사각형에 최대 1개의 동전을 올려 놓습니다. 은화로 불리는 동전 하나만 가치가 있습니다. 두 명의 선수가 차례대로 수를 둡니다. 각 차례에 일반 또는 특수 이동 둘 중 하나를 해야만 합니다.

일반 이동은 동전 하나를 선택하고 왼쪽으로 하나 이상 떨어진 정사각형으로 옮기는 것입니다. 동전은 띠를 벗어나지 못하고 다른 동전 위로 올라가거나 다른 동전을 넘어갈 수도 없습니다.

일반 이동 대신, 특수 이동을 할 수도 있는데 이는 가장 왼쪽 동전을 주머니에 넣는 것입니다. 만일 어떠한 일반 이동도 가능하지 않다면, 가장 왼쪽 동전을 주머니에 넣어야만 합니다.

이 게임의 승자는 은화 동전을 먼저 주머니에 넣는 선수입니다.

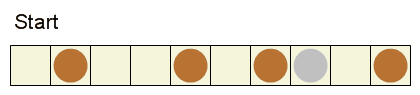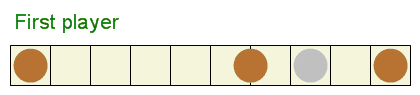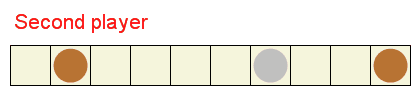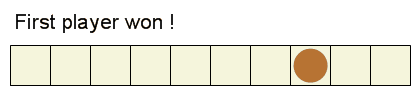
승리하는 구성은 두 번째 선수가 어떻게 하더라도 첫 선수가 승리를 강제할 수 있는 동전 배치입니다.

W(n,c)를 c개의 가치 없는 동전과 하나의 은화 동전이 배치된 정사각형 n개의 띠에서 '승리하는 구성'의 수라고 합시다.

W(10,2) = 324 이고 W(100,10) = 1514704946113500 입니다.

W(1 000 000, 100)를 구하고 그 값을 반소수 1000 036 000 099 (= 1 000 003 · 1 000 033)로 나눈 나머지를 답으로 제출하세요.