3차 베지어(Bézier) 곡선은 다음 네 점으로 정의합니다: P₀, P₁, P₂ 그리고 P₃입니다.

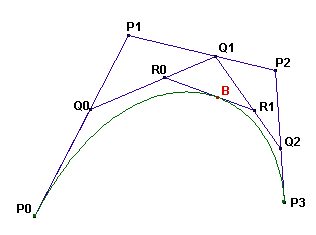
베지어 곡선은 아래와 같이 작성됩니다:

세 선분 P₀P₁, P₁P₂ 그리고 P₂P₃ 위에 세 점 Q₀,Q₁ 그리고 Q₂를 다음 조건과 같이 그립니다
P₀Q₀ / P₀P₁ = P₁Q₁ / P₁P₂ = P₂Q₂ / P₂P₃ = t (t는 범위 [0,1]의 어떤 실수입니다).

이제 선분 Q₀Q₁ 과 Q₁Q₂ 위에, 두 점 R₀ 와 R₁를 다음과 조건과 같이 그립니다
Q₀R₀ / Q₀Q₁ = Q₁R₁ / Q₁Q₂ = t (t는 위와 동일한 값입니다).

선분 R₀R₁ 위에 R₀B / R₀R₁ = t(t는 여전히 위와 동일한 값입니다)가 되는 점 B를 그립니다.

네 점 P₀, P₁, P₂, P₃으로 그리는 베지어 곡선은 선분 P₀P₁ 상의 점 Q₀가 선분을 이동하면서 만드는 B의 자취로 정의 됩니다.
(모든 계산에서 t의 값은 항상 동일해야 함에 주의하세요.)

위 작성법에서, 베지어 곡선은 점 P₀에서 선분 P₀P₁에 접하고 점 P₃에서 선분 P₂P₃에 접하는게 명백합니다.

네 점 P₀=(1,0), P₁=(1,v), P₂=(v,1) 과 P₃=(0,1)로 정의되는 3차 베지어 곡선을 이용해 사분원에 유사하게 만들 수 있습니다.
두 선분 OP₀, OP₃ 과 베지어 곡선이 이루는 영역의 면적이 (사분원의 면적인) ^π/₄이 되도록 v > 0의 값을 정합니다.